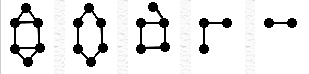
Subgraphs

A subgraph S of a graph G is a graph whose set of vertices and set of edges are all subsets of G. (Since every set is a subset of itself, every graph is a subgraph of itself.)

All the edges and vertices of G might not be present in S; but if a vertex is present in S, it has a corresponding vertex in G and any edge that connects two vertices in S will also connect the corresponding vertices in G. All of these graphs are subgraphs of the first graph.

A vertex-induced subgraph is one that consists of some of the vertices of the original graph and all of the edges that connect them in the original. An edge-induced subgraph consists of some of the edges of the original graph and the vertices that are at their endpoints.

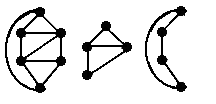	The second two figures are vertex-induced subgraphs of the first figure.
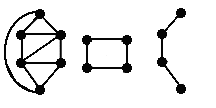	The second two figures are edge-induced subgraphs of the first figure.

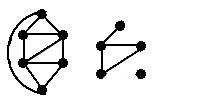The second figure is a subgraph of the first figure, but it is neither edge-induced nor vertex-induced.

A spanning subgraph is a subgraph that contains all the vertices of the original graph. A spanning tree is a spanning subgraph that is often of interest. A cycle in a graph that contains all the vertices of the graph would be called a spanning cycle. However it's more common name is a Hamiltonian cycle.

Copyright © 1999-2000 SciMathMN