Sets

From a theoretical point of view, sets can be considered the building blocks of mathematics.

The term set is usually taken to be an undefined primitive term; intuitively, it means a collection, or a group, of objects: numbers, shapes, balls, trees, people, etc.

Another undefined term is element, referring to each object in a set. We say that each element is in, or is a member of, the set, and that the set contains its elements.

A set is considered to contain each of its elements only once. The sets {a, b, b, c} and {a, b, c} are considered the same. To model situations in which repetition occurs, such as counting with replacement, a sequence can be used. Since sequences naturally put elements in order, sometimes the construct of a multiset is invoked, meaning a sequence without order.

One set is a subset of another if all the elements of the one are also in the other. By this definition, every set is a subset of itself. One set is a proper subset of another if the first is a subset that's not all of the second.

Also following from the definition of subset, a set with no elements is a subset of every other set, since every element that is in the set with no elements is in any other set. The set with no elements is called the empty set or null set.

Combining sets

The intersection of two streets consists of the points that are common to the streets. Similarly, the intersection of a collection of sets is the subset of all of the sets that contains the elements common to all sets in the bunch. If the sets contain no common elements, the intersection is the empty set.

Two sets whose intersection is the empty set—that is, sets that don't overlap—are said to be disjoint.

The union of a collection of sets contains all elements that are in any of the sets. Each set in the collection of sets is a subset of the union.

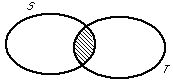
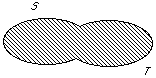
To help visualize intersection and union, we often use Venn diagrams.

The shaded part of this Venn diagram represents the intersection of sets S and T:
The shaded part of this Venn diagram represents the union of sets S and T:

Defining intersection and union can be a little confusing. The temptation is to say that the intersection of S with T is S and T, and the union is, well, S and T also. A more careful way of defining the terms is by saying that the intersection of two sets is the set of elements that are in both, and the union is the set of elements that are in either or both. Saying either or both gets to be tiresome, though, so mathematicians (and logicians) use the word or to mean and/or and say

The union of sets S and T is the set of elements that are in S or in T.

The intersection of sets S and T is the set of elements that are in S and in T.

Here's a Venn diagram whose shaded part represents the difference between sets S and T: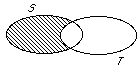

A partition of a set is a collection of subsets that might be said to "divide the set into pieces." The union of the subsets is the entire set, and no two of the subsets have common elements.

Size

The size of a set is the number of elements in the set. That number is also called the cardinality, or order, of the set. You can define size more carefully by saying that a set has size n if there's a bijection between the set and the set of positive integers {1, 2, . . . , n}.

This definition applies to finite sets. In fact, a set can be defined as finite if there's a bijection between it and some set of positive integers {1, 2, . . . , n}. An infinite set is then a set that's not finite.

Alternatively, an infinite set can be said to be a set from which there's a bijection to a proper subset of itself.

Sets, and especially infinite sets, have led to a variety of paradoxes since the late 1800s.

Copyright © 1999-2000 SciMathMN