Graphs, vertices, and edges

Formally, a graph consists of a finite nonempty set, whose elements are the vertices (or nodes) of the graph, together with a (possibly empty) set of unordered pairs of distinct vertices called edges (or arcs). (A single one of the vertices is called a vertex.)

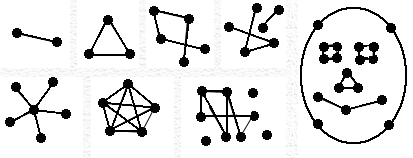
A graph can be represented as a picture consisting of dots and line segments. The dots represent the graph's vertices, and the lines represent the edges.

A graph might be represented by quite different-looking pictures. For example, in one drawing of a graph, two edges might intersect at points other than vertices, whereas in another picture of the same graph no edges are drawn as crossing.

Here are some pictures of graphs.

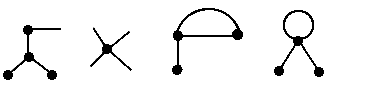
Notice that every edge begins and ends on a vertex. Every edge must have exactly one vertex at each of its endpoints. Moreover, by our definition of graph, no two vertices may share more than one edge, and no single vertex can serve as both endpoints of an edge. So none of these pictures represents a graph:

Note that the graphs that are the subject matter of graph theory are unrelated to graphs of equations in algebra or graphs that are used to chart data.

Often it's useful to label vertices of a graph with letters. An edge connecting two vertices is described using the letters of the endpoints. For example, the edge connecting vertices labeled C and J is called CJ or JC.

Sometimes the term network is used synonymously with graph, but usually a network is a special kind of graph. This lack of consistency in terminology reflects the relatively short history of graph theory. For other examples, see pseudograph and multigraph.

Copyright © 1999-2000 SciMathMn