The indegree of a vertex in a digraph is the number of edges entering (pointing to) that vertex. The outdegree of the vertex is the number of edges leaving (pointing away from) that vertex.
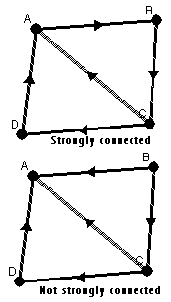
Sometimes a digraph is called an oriented graph. The simple graph from which the digraph is drawn is called the underlying graph. Sometimes a digraph is referred to as an orientation of the underlying graph.
In addition, an edge can be referred to as oriented or having an orientation. In graph theory, either all or none of the edges of a graph will be oriented.