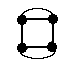
 In the picture to the left, two sets of vertices are connected by more than one edge. Multigraphs may include such "parallel" edges. In our terminology a graph is a special kind of multigraph.
In the picture to the left, two sets of vertices are connected by more than one edge. Multigraphs may include such "parallel" edges. In our terminology a graph is a special kind of multigraph.Pseudographs and multigraphs
These tours use the word graph to include graphs in which at most one edge connects any two vertices. Some mathematicians use a broader definition of graph.
 In the picture to the left, two sets of vertices are connected by more than one edge. Multigraphs may include such "parallel" edges. In our terminology a graph is a special kind of multigraph.
In the picture to the left, two sets of vertices are connected by more than one edge. Multigraphs may include such "parallel" edges. In our terminology a graph is a special kind of multigraph.
Giving the endpoints of an edge in a multigraph may not be enough to distinguish it. Often the edges as well as the vertices are labeled, and a walk is described as an alternating sequence of vertices and edges.
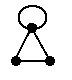 In the picture to the right, an edge connects a vertex to itself. That edge is called a loop. Loops are possible in a pseudograph. Pseudographs may also include multiple edges between vertices, so multigraphs are special cases of pseudographs.
In the picture to the right, an edge connects a vertex to itself. That edge is called a loop. Loops are possible in a pseudograph. Pseudographs may also include multiple edges between vertices, so multigraphs are special cases of pseudographs.
A formal definition of pseudograph refers to a set of vertices, but the edges are defined as a sequence of pairs of vertices. If the definition called for a set of edges, then no pair of vertices could have more than one edge, because elements can't occur more than once in a set.
Ordinarily, when we use the term graph, we are excluding pseudographs and multigraphs. Sometimes, for clarity's sake, we use the term simple graph instead of the term graph.
Copyright © 1999-2000 SciMathMN