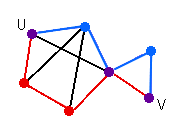
Two paths from U to V

A trail from U to V
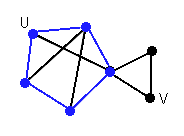
Walks: paths, cycles, trails, and circuits
A walk is an alternating sequence of vertices and connecting edges.
Less formally a walk is any route through a graph from vertex to vertex along edges. A walk can end on the same vertex on which it began or on a different vertex. A walk can travel over any edge and any vertex any number of times.
| A path is a walk that does not include any vertex twice, except that its first vertex might be the same as its last. |  Two paths from U to V |
| A trail is a walk that does not pass over the same edge twice. A trail might visit the same vertex twice, but only if it comes and goes from a different edge each time. |  A trail from U to V |
| A cycle is a path that begins and ends on the same vertex. |  |
| A circuit is a trail that begins and ends on the same vertex. |  |
For digraphs, walks can travel edges only in the direction of the arrows.
Copyright © 1999-2000 SciMathMN