Graph Concepts

Hamiltonian cycles and Hamiltonian paths

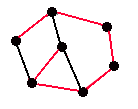
A Hamiltonian path is a path that visits every vertex once and only once, except that it might (or might not) begin and end at the same vertex.

Hamiltonian path

A Hamiltonian cycle is a Hamiltonian path that begins and ends on the same vertex and visits all the other vertices in the graph exactly once. A Hamiltonian cycle does not necessarily traverse every edge in the graph.

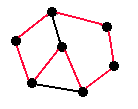Hamiltonian cycle Hamiltonian cycle

A graph is called Hamiltonian if it contains a Hamiltonian cycle.

The term Hamiltonian is derived from the name of the Irish mathematician William Rowan Hamilton who designed and marketed a puzzle whose solution essentially required finding a Hamiltonian cycle in a graph.

On the surface, a Hamiltonian cycle may seem to be very much like an Eulerian circuit, but they are actually quite different. A graph that has an Eulerian circuit may or may not also contain a Hamiltonian cycle, and vice versa.

One well-known problem involving Hamiltonian cycles is the problem of finding a minimal Hamiltonian cycle in a weighted graph. this problem is also known as the Traveling Salesperson Problem or TSP because a solution to this problem answers a question commonly asked by traveling salespeople: What is the most efficient route that I can take to visit all of my clients?