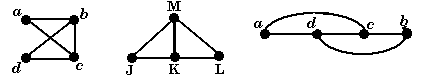
Isomorphic graphs and pictures
Two graphs are isomorphic when the vertices of one can be re labeled to match the vertices of the other in a way that preserves adjacency.
More formally,
A graph G1 is isomorphic to a graph G2 if there exists a one-to-one function, called an isomorphism, from V(G1) (the vertex set of G1) onto V(G2 ) such that u1v1 is an element of
E(G1) (the edge set of G1) if and only if u2v2 is an element of G2.
The opposite of isomorphic is non-isomorphic.
(Refer to "Different pictures" in Abstractions of the Sly Spy tour to explore the subtle differences between a graph and a picture of a graph.)
No way is known for quickly testing two graphs to determine if they are isomorphic. You can be assured that two graphs are isomorphic if you can "morph" a picture of one graph to match a picture of the other, except for vertex labels. Or you can be sure the graphs are isomorphic if you can label vertices consistently in a list of edges of one graph to come up with a list of edges in the other.
The three graphs pictured below are isomorphic, but they are not the same graph. As the first picture is morphed into the second, the labels don't match. One isomorphism takes a to J, b to K, c to M, and d to L. Although the letters on the first and third pictures are the same, they do not represent the same graph. An isomorphism takes a to a and c to c but interchanges b and d.
How do we know they are not isomorphic?
Unfortunately, a failure to redraw the pictures to look alike, or to discover a way to change labels while preserving adjacencies, does not necessarily mean that the graphs are not isomorphic. It could mean that you just haven't tried hard enough yet!
You can be certain that two pictures are not isomorphic if they don't have same number of vertices and edges. In addition, two graphs that are isomorphic must have the same degree sequence. Be careful, however, because it is also possible for two graphs with the same degree sequence to be non-isomorphic.
Two graphs cannot be isomorphic if one of them contains a subgraph that the other does not.
 |
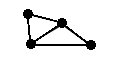
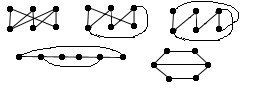
The two graphs pictured here have the same degree sequence but they are not isomorphic because only one of them contains a subgraph isomorphic to this graph: |
 |
Related to the notion of isomorphic graphs is the fact that a single graph can have lots of different pictures. The ideas are related in two ways:
There is a subtle distinction between the idea of two graphs being isomorphic and two graphs that are the same. Because of the closeness of concepts, people often say that two pictures are isomorphic graphs, even if by the definitions they're actually different drawings of the same or isomorphic graphs. This terminology is so common that below we'll write isomorphic pictures as shorthand for pictures of the same graph.
To decide whether or not two pictures are isomorphic, it's useful to imagine that the edges of a graph are infinitely stretchable and pliable. A picture can be changed by tugging or crisscrossing the edges in any way, even across other vertices or edges. As long as no edge is disconnected from the vertices at its endpoints, the resultant picture will be isomorphic to the first.
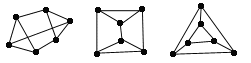
These three pictures are isomorphic.
This animation shows how the first picture can be morphed in the second picture of the same graph.
(Click on the square to see how one picture can be morphed into another picture of the same graph. Click on the animation to stop or restart it.)
This animation shows that the third picture is of the same graph as the others.
It is not particularly easy to tell at a glance whether or not two pictures are isomorphic. As you work with more and more graphs, however, you will develop a facility, even an intuitive feel, for the underlying graph.
Copyright © 1999-2000 SciMathMN