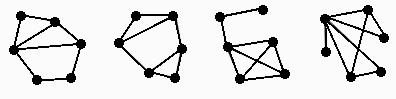
Some graph vocabulary: join, adjacent, incident, complete, size, order

When two vertices of a graph are connected by an edge, these vertices are said to be adjacent, and the edge is said to join them.

When two edges meet at the same vertex, those two edges are said to be adjacent.

A vertex and an edge that touch one another are said to be incident to one another. Each is said to be on the other.

The term size refers to the number of edges in a graph. The number of vertices in the graph is called its order.

Each of these graphs is of order 6 and size 8. By a common notational convention, these graphs are referred to as (6,8) graphs.

A complete graph is a graph in which all vertices are adjacent to one another.

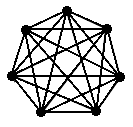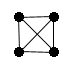
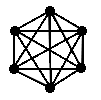
K(4)	K(5)	K(6)	K(7)

Thus, in a complete graph, every possible edge is present. A complete graph on n vertices is denoted as K(n). Thus K(3) is the complete graph on 3 vertices, K(4), the complete graph on 4 vertices, etc.

A trivial graph is a graph with a single vertex. All other graphs are nontrivial.

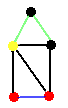This is a (5,7) graph. It has order 5 and size 7. The two green edges are adjacent. The two red vertices are adjacent; they are joined by the blue edge. The blue edge is incident on the red vertices. The degree of the yellow vertex is 4. This is not a complete graph because not all the vertices are adjacent.

Copyright © 1999-2000 SciMathMN