Graph Concepts

Degree, regular, degree sequence

The degree of a vertex is the number of incident edges it has.

The First theorem of graph theory relates degrees to edges. It states that the sum of the degrees of the vertices is twice the number of edges.

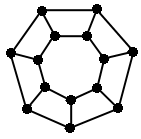
If every vertex of a graph has the same degree, then that graph is called regular. In an n-regular graph, all vertices have degree n.

2-regular Thus, in a 2-regular graph, all vertices have degree 2.

In a 3-regular graph, sometimes called a cubic graph, all vertices have degree 3.

4-regular In a 4-regular graph all vertices have degree 4, and so forth.

The degree sequence is a non-increasing sequence of the degrees of the graph’s vertices.

vertex degrees For example, the table beside the graph at the left lists the degree of each vertex.

When the numbers in the degree column are rearranged into non-increasing order, the list becomes: 4, 4, 3, 3, 2, 2, 1, 1, 1, 1. This is the degree sequence for the graph.