Coloring

A number of interesting problems and applications can be explored by experimenting with ways to color either the edges or the vertices of a graph. When the problem or application involves coloring the vertices of a graph, the choice and arrangment of the colors is called a vertex-coloring. An edge-coloring of a graph refers to the choice and arrangement of colors for the edges.

An edge-colored graph	A vertex-colored graph

Formally, a vertex coloring of a graph is a one-to-one function from the set of the graphs's vertices into the set of all colors. An edge coloring is defined similarly.

The minimum number of colors required for a vertex coloring with no adjacent vertices colored the same color is called the vertex-chromatic number or simply the chromatic number of the graph. The edge-chromatic number is the minimum number of colors that are required for an edge coloring with no adjacent edges colored the same color.

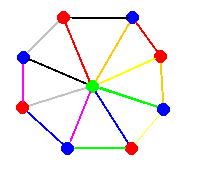A graph with edge-chromatic number 8 and vertex-chromatic number 3.

An historically important theorem about finding the vertex-chromatic number of a graph grew out of the Four-color conjecture, which claims that every planar graph can be vertex-colored with four or fewer colors.
Copyright © 1999-2000 SciMathMN