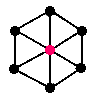
radius = 1
center is red
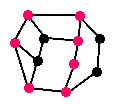
radius = 3
centers are red
Graph measurements: length, distance, diameter, eccentricity, radius, center
A graph's edges are stretchable, so you can't measure distances in a graph with linear measures such as inches or centimeters. When you look at a graph, however, you can still sense that some parts of the graph are “farther apart” than others. The following terms help us quantify and speak precisely about these notions:
The length of a walk (path, cycle, circuit or trail) in a graph is the number of edges it contains.
The distance between two vertices is the length of the shortest, or minimal, path between them. (The notion of distance applies only to connected components of graphs.)
The diameter of a graph is the longest distance you can find in the graph. It is a measure of the length of the longest minimal path. (A path is not minimal if the two vertices at its endpoints could be connected by a shorter path.)
If a graph has a diameter, then shouldn't it also have a radius? And if it does, what would the radius be?
The diameter of a graph is somewhat like the diameter of a circle, if you consider the diameter of the circle to be the distance across the circle at its fattest point. If you think of the term radius as meaning "half the diameter" as it does for circles, it's hard to find a clear analog for the idea of radius in a graph. Consider instead that the radius of a circle is the distance from the center to the outer edge. We can stretch and bend this concept into that of the radius of a graph.
To do this we must ask: What could the center of the graph be? How far away from the center can you always go without "running out" of graph? An intermediate idea, that of eccentricity, helps develop these ideas.
The eccentricity of a vertex is the length of the longest minimal path from that vertex to some vertex in the graph. You can think of the eccentricity of a vertex as the longest distance in the graph from there to somewhere.
The center of a graph is the collection of vertices (called the central vertices) whose eccentricity is least. In other words, it's the collection of vertices whose longest distance to all other vertices is the smallest.
The radius of a graph is the length of the shortest eccentricity in the graph. It's the eccentricity of each central vertex. Imagine there is a graph on the floor. You will be plopped over and over again on some arbitrary vertex on the graph from which you must travel. Each time this happens you will always travel the same distance. It is up to you to choose (once and for all, after you've seen the graph of course) what this distance will be. You will be given a dollar for every edge that you travel. However, if, at any time, after traveling your required distance you end up closer to where you started than you would have been had you traveled a shorter distance, you will forfeit all your winnings and be thrown out of the game. What distance should you choose to win the most possible money?
(Unless the game terminates, anyone who chooses a distance less than or equal to the radius will win an infinite amount of money. Where do I sign up to play?)
 |
diameter = 2 radius = 1 center is red |
 |
diameter = 4 radius = 3 centers are red |
The radius of G is less than or equal to diameter of G is less than or equal to twice the radius. How is it conceptually the same and not the same as d = 2r?
Copyright © 1999-2000 SciMathMN