Vertex connectivity and edge connectivity

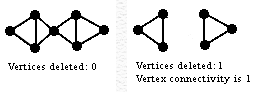
To determine the vertex connectivity of a graph, we ask the question: what is the minimum number of vertices that we must remove from the graph to disconnect it?

Since, by definition, an edge connects two vertices, when a vertex is removed from a graph, all of the edges incident with that vertex must also be removed. These edges cannot be arbitrarily connected to other vertices.

This graph has vertex connectivity of 1:

This graph has vertex connectivity of 3:

This graph has vertex connectivity 5:

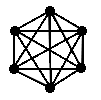
You cannot split a complete graph into two disconnected components by simply removing vertices. Removing successive vertices ultimately reduces the graph to a single vertex. So for complete graphs, the connectivity is measured by counting the number of vertices that must be removed to reduce the graph to a single vertex.

To determine the edge connectivity of graph, we ask the question, what is the minimum number of edges that we can remove from the graph to disconnect it?

This graph has edge connectivity of 1:
This graph has edge connectivity of 2: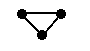
This graph has edge connectivity of 3: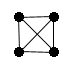

Notice that deleting an edge from a graph does not require you to delete any vertex in the way that deleting a vertex requires you to also delete the incident edges.

Copyright © 1999-2000 SciMathMN