MATtours of discrete mathematics

Initiators and generators in fractal images

Fractals are defined in terms of initiators and generators. The initiator is the object with which one begins, and the generator is a rule for modifying the initiator. The generator modifies the initiator in such a way as to produce an object which contains one or more new copies of the initiator, and then the generator rule is reapplied to those copies of the initiator. Theoretically the process continues infinitly, much like a "hall of mirrors."

Thus a fractal is an abstract mathematical object which cannot be represented in any concrete fashion. With computer graphics, however, hundreds, thousands, or even millions of applications of the generator rule can be represented so that intricate and extremely complex approximations of the abstract object can be viewed.

A Sierpinski gasket is a fractal image whose initiator is a regular polygon—in this case, an equilateral triangle.

The generator rule can be remove from the center of that triangle the equilateral triangle formed by connecting the midpoints of the sides of the original triangle. stage 1

This leaves three smaller copies of the initiator (equilateral triangles) to which the generator rule can be applied again. stage 2

A Sierpinski gasket is the (abstract) object which results when this process is repeated an infinite number of times.

Here is another Sierpinski gasket whose initiator is a square and whose generator rule is to remove the square consisting of the left uppermost quadrant of the initiating square.

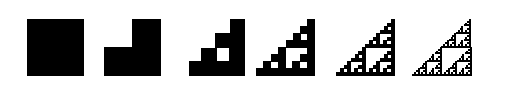
A Sierpinski gasket is a fractal image whose initiator is a regular polygon—in this case, an equilateral triangle.
The generator rule can be remove from the center of that triangle the equilateral triangle formed by connecting the midpoints of the sides of the original triangle.
This leaves three smaller copies of the initiator (equilateral triangles) to which the generator rule can be applied again.