Inclusion/exclusion principle

The inclusion/exclusion principle is a counting technique that relates information about the number of elements in a set, its subsets, and the intersections of those subsets:

In a set with some subsets that intersect in some way (possibly not at all), the number of elements that are not in any of the subsets will equal:

the number of elements in the original set
minus the sum of the numbers of elements in all of the subsets,
plus the sum of the numbers of elements in the intersections of all pairs of the subsets
minus the sum of the numbers of elements in the intersections of all triples of the subsets
plus the sum of the numbers of elements in the intersections of all quadruples of the subsets
plus. . . minus. . .

Here is an example:

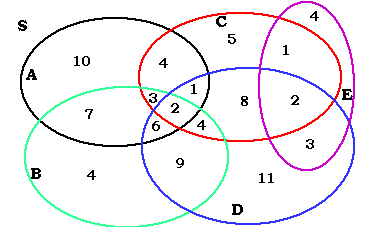
The Venn diagram below illustrates a set S, which contains 90 elements and 5 subsets, A, B, C, D, and E.

A	33	intersection of A, C, D	3
B	35	Intersection of A, D, E	0
C	30	intersection of A, B, D	8
D	46	intersection of A, B, E	0
E	10	intersection of A, C, E	0
A intersection B	18	intersection of A, D, E	0
A intersection C	10	intersection of B, C, D	6
A intersection D	9	intersection of B, D, E	0
A intersection E	0	intersection of B, C, E	0
B intersection C	9	intersection of C, D, E	0
B intersection D	21	intersection of A, B, C, D	2
B intersection E	0	intersection of A, B, C, E	0
C intersection D	17	intersection of A, B, D, E	0
C intersection E	3	intersection of A, C, D, E	0
D intersection E	5	intersection of B, C, D, E	0
intersection of A, B, C	5	intersection of A, B, C, D, E	0

Therefore, there are 6 element in S not in A, B, C, D, or E.

Copyright © 1999-2000 SciMathMN