Coordinates and coordinate graphs

A coordinate pair is an ordered pair of real numbers, usually used in describing a point on the plane. The first number of the pair gives a distance in one direction from a point called the origin, and the second number gives a distance in another direction. If you go from the origin in the first direction the distance specified by the first coordinate, and then from that point go in the second direction the distance specified by the second coordinate, you'll get to a point on the plane. As long as the directions aren't the same as or opposite to each, each point in the plan corresponds to a unique coordinate pair.

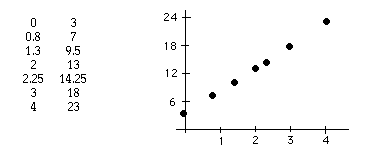
A coordinate graph of a set of coordinate pairs is the set of points representing those pairs. For example, the graph to the right below represents the set of ordered pairs given in the table to its left, assuming that the direction of the first coordinate is to the right of the origin and the direction of the second coordinate is upward.

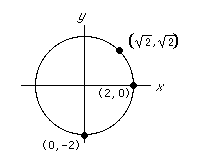The graph of an equation is the set of points representing all ordered pairs that satisfy the equation. For example, the equation
x² + y² = 4 is satisfied by infinitely many ordered pairs such as

(2, 0),

(0, –2), and

A graph of the infinitely many points representing those pairs is given by the circle in the picture to the right, if the two directions specified are perpendicular to each other. In the case of perpendicular directions, the coordinates are called rectangular coordinates.

A different way of using coordinates to represent points on a plane is by fixing not only an origin (called the pole) but a ray emanating from the origin. The first coordinate can give a distance along the ray, and the second coordinate can give an angle to move counterclockwise (anticlockwise) relative to that ray. These coordinates are called polar coordinates.

Coordinate pairs can describe points on surfaces other than the plane. They were used as long as 4000 years ago as the Babylonians and Classical Greeks tried to describe points in the sky and on the spherical earth. On the earth, with the origin taken as a fixed point on the equator, the first coordinate could describe the distance moved eastward along the equator, and the second coordinate could describe the distance moved northward. Now we refer to these coordinates as the longitude and latitude of a point.

Ordered triples can be used to describe points in three-dimensional space. In the rectangular system, an origin and three mutually-perpendicular directions are specified. The cylindrical system generalizes polar coordinates by adding a direction in a direction perpendicular to the plane of the pole and ray. Spherical coordinates include two angles and one distance.

Copyright © 1999-2000 SciMathMN