Derivation of polar coordinate equation of ellipse

What's the equation of an ellipse in polar coordinates?

The standard approach to finding polar coordinate equations from known rectangular coordinate equations is to do the substitution

It would be nice if we could simplify that square root in the denominator, wouldn't it?

Anyway, you can use a graphing calculator or computer software to check the validity of this equation.

With rectangular coordinates we were successful placing the origin at the center of the ellipse, although we had the fleeting through that it might work better to put the origin at a focus. Perhaps we would get a simpler polar coordinate equation if we put the center at a focus. Let's choose the left focus, assuming that the major axis is horizontal. We get this picture:

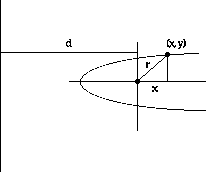
From the constant ratio property we know that the eccentricity e equals

That was simple! Because it doesn't have a square root, this polar coordinate equation for an ellipse may be preferable to the one we found before.

But this version of the equation involves d, the distance from the focus to the directrix, which isn't a number that arises commonly when discussing ellipses. The most common values are a , b , and c . Can we get an equally simple equation by straight substitution into the rectangular coordinate equation if we assume that the origin is at the left focus?

In that case, our figure is shifted c units to the right, so the equation is

We have found a polar coordinate equation for an ellipse using only variables a , b , and c .