Dandelin's "ice-cream-cone" proof of the constant sum property

We assume that an ellipse is a figure satisfying the conic section property. We write a virtually identical proof assuming the cylindrical section property with less notation.

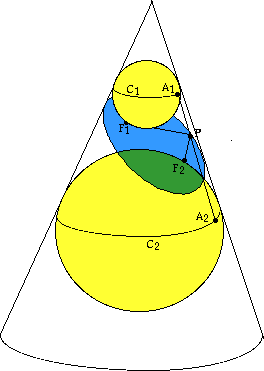
Among all of the spheres that fit inside the cone, each tangent to the cone along a horizontal circle, there are two that are tangent to the intersecting plane, one on each side of it. Call the points where the spheres are tangent to the plane F₁ and F₂. These will be the foci. Call the circles where the spheres are tangent to the cone C₁ and C₂. The distance from C₁ to C₂ along any generator of the cone will be constant.

Let P be an arbitrary point on the ellipse. Consider the cone generator through P, and let the points where it intersects C₁ and C₂ be A₁ and A₂, respectively. Then the distance from P to F₁ is the same as the distance from P to A₁ because PF₁ and PA₁ are tangents from P to the same sphere. For the same reason, the distance from P to F₂ equals the distance from P to A₂. Therefore the sum of the distances from P to F₁ and F₂ is the distance from A₁ to A₂, which is a constant independent of P.