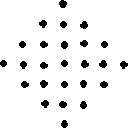
Tree farm
Here is a view of a tree farm from above. How many ways can you determine the number of trees?

Approaches
counting one at a time
Can you find an easier way?
grouping in some way
for example, 6 x 4 + 1
adding rows
1 + 3 + 5 + 7 + 5 + 3 + 1 1 + 1 + 3 + 3 + 5 + 5 + 7
combining rows or columns
(1 + 7) + (3 + 5) + (5 + 3) + 1 = 3 x 8 + 1 2 x (1 + 3 + 5) + 7 = 2 x 9 + 7
adding diagonals
4 + 3 + 4 + 3 + 4 + 3 + 4
using squares
The 4 diagonals of 4 dots form one square and the 3 diagonals of 3 dots form another, to get 4 x 4 + 3 x 3.
Respond: Is this the same as adding diagonals? Elicit ideas of multiplication as repeated addition, commutativity
breaking into pieces
middle column (7) + middle row (6 more) + 4 x 3 in each corner)
using symmetry
by horizontal or vertical reflection symmetry, 2 x 9 + 7
by diagonal reflection symmetry, 2 x 11 + 3
introduce idea of reflective, or mirror, symmetry
Rewrite all approaches as number sentences.
Compare number sentences. What properties of arithmetic say that these sentences are equivalent?
Your experience
Have you used this problem with a class and seen approaches other than(or more specific than) those mentioned above? Or do you have other comments or criticisms or stories? If so, please tell us!
Last updated 30 November, 2004