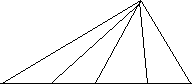
Dividing triangles

Find as many ways as you can to divide an arbitrary triangle into four equal-area triangles. (Scher, Daniel, "A Triangle Divided: Investigating Equal Areas," Mathematics Teaching 93, 7, 10/00, p. 608. Problem taken from Connected Geometry (EDC 2000))

Approaches

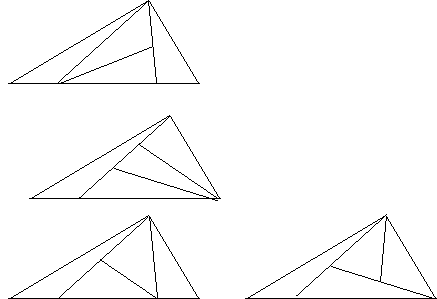
Quarter any side and join quartiles to opposite vertex (3 ways for 3 sides)

Draw any of the three medians, then subdivide the halves into halves (up to 27 ways).

Ignoring a quarter, subdivide the rest into three pieces.

Turn into equivalent rectangle, partition the rectangle, and rearrange pieces into the original triangle.

Your experience

Have you used this problem with a class and seen approaches other than(or more specific than) those mentioned above? Or do you have other comments or criticisms or stories? If so, please tell us!

Last updated 30 November, 2004