Warehouses

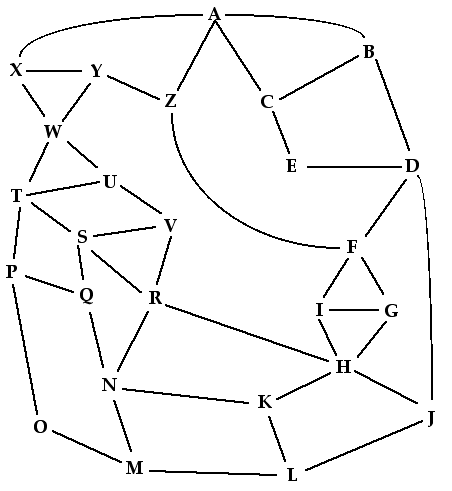
In the picture below, each letter represents a city at which your company plans to have retail stores. The lines represent connecting plane routes between those cities. The company wants to build warehouses to service those stores. The goal is to establish warehouses in a way that every city with a retail store is within one flight of some warehouse. Of course, the company wants to build as few warehouses as possible. In what cities should it put warehouses? (Idea and graph originally from Nancy Casey.)

Alternatives

For young children, the edges can be streets in a town, whose council is trying to decide where to put fire stations so that every corner is within one block of a station. They don't want to build any more stations than needed so that they'll have money left over to build a swimming pool. (This was Casey's original problem, for second graders.)

Approaches

Mark with pen or pencil.

Mark with coins or poker chips or bingo chips.

Randomly, getting 10-12 locations for warehouses.

Can you do it with fewer?

Put at nodes with lots of edges.

Let groups overhear each other getting down to seven and then six markers. Point out how an intuitive feel for the map eventually overrides initial intuitions, as is often the case in doing mathematics.

Your experience

Have you used this problem with a class and seen approaches other than(or more specific than) those mentioned above? Or do you have other comments or criticisms or stories? If so, please tell us!

Last updated 30 November, 2004