Stars and circles

In a hat there were three cards. One had a star on both sides. One had a circle on both sides. And the third had a star on one side and a circle on the other. You pulled out one of the cards at random and placed it on a table. The face that's up has a star on it. What's the probability that the face that's down also has a star? (Adapted from problem in Interactive Mathematics Program (IMP), year 1)

Logistics

Arguments about this can become very passionate.

You might actually prepare a set of three cards for each group.

Approaches

The probability is 1/2, since you know that you got one of two cards and they are equally likely, but only one of the two has a star on the reverse side.

The probability is 2/3, since there are three sides that are equally likely to be facing up, and in two of the three cases there's a star on the reverse side.

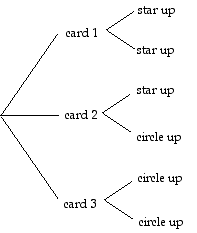
A tree diagram like the one to the right shows that, of the six outcomes, our attention is limited to three, two of which come from the card that has a star on both sides.

A calculator simulation depends on whether the person doing it assumes that the two cards or the four sides are equally likely.

Apply Bayes's Rule to get 2/3.

Kyle's Iron Law of Probability: Whenever your intuition tells you the answer is 1/2, the answer is 2/3.

The probability is 0 or 1, because the card is chosen and lying there. You just don't know yet whether the probability is actually 0 or actually 1.

Your experience

Have you used this problem with a class and seen approaches other than(or more specific than) those mentioned above? Or do you have other comments or criticisms or stories? If so, please tell us!

Last updated 30 November, 2004