The Age of Computation
Many ideas in this article come from Douglas Campbell, The Whole Craft of Number (Boston: Prindle, Weber, & Schmidt, 1976).
Imagine living before -600 with a nomadic tribe and spending most of your time hunting or herding. Occasionally you compare your flock of sheep with a pile of pebbles to be sure that no sheep have been lost. Maybe you have names for the numbers we call one, two, and three, but more than three you call many. You probably have a map in your head of where important geographical landmarks are located relative to each other. Sometimes the shaman of your tribe draws pictures in the dirt representing the sun and moon and elk, to bring about good weather or happy hunting. You and your neighbors represent reality through some simple symbols: stones, maps, pictures.
Every cloudless night there is this fantastic light show. In the summer you go out and lie in the grass and stare for hours up at the big screen in the sky. Most of the show is pretty much the same from night to night; the points of light move in the same way through the evening. You never tire of finding shapes among them. Perhaps you imagine a hunter chasing animals across the heavens. There are a few lights, though, that move differently from the others. Some nights they'll be in one part of the sky and some in another. You call these lights the wanderers, or planets.
You also find that you can create beauty in paintings and by decorating pottery. You discover how different shapes make objects more beautiful. You especially like shapes that are symmetric. And perhaps you begin to phrase in your head an important problem:
What is symmetry?
This is a problem mathematicians will work on
for centuries.
Or imagine that you live in an agricultural community.
You enjoy looking at the sky, too. You have names
for larger numbers, also, since they're needed for trading.
You know some recipes for making complicated foods
like bread. You compare quantities of objects, and
you have a vague notion of relative sizes of fields
and volumes of harvests. Instead of one stone for
each sheep, you save space by replacing five regular
stones with one special red stone, and five red stones
with a white stone. And the shaman of your tribe actually
draws pictures representing the stones, which were
representing the sheep. That is, your tribe has symbols
to represent symbols.
You are interested in the sizes of plots of agricultural
land. And you want to be able to compare those sizes.
You phrase a second major problem of mathematics:
How can we find the size of any shape?
Little do you imagine that this problem will be a major question of the branch of mathematics called calculus.
Or imagine living later, as part of a larger political system. Such large collections of people, united by conquest, existed in China, India, Egypt, Mesopotamia, and Central America. They had alphabets, ships, and metals, creating an economy based on trading, and not just trading agricultural products.
You are part of the huge bureaucracy that runs the system. At the top might be an Emperor. Your boss is the local viceroy. Your job is to provide your boss with information. You use a system that systematically gives names to large numbers, so that the population can be counted. To levy taxes you compute the areas of pieces of land and do arithmetic with the resulting numbers. You work with geometric forms to help design large buildings for the Emperor. To make recommendations about when planting should occur and when rivers will flood, you must know about weather patterns and the calendar. And sometimes you just don't explain how you figure out some things. People seem to give you more respect if they think that your god told you when the winter solstice would be coming. Moreover, if you announce that your god is unhappy and needs appeasing, people can be persuaded to give you gifts.
If you live in Mesopotamia, you have access to lists of information compiled by your predecessors. If the viceroy asks you for the cost of outfitting a crew of slaves, workers, and supervisors to build a building, you can look up in a table the numbers of each kind of person and read off the cost without doing a lot of calculation. The computations have been done in advance.
You even have some time to mess around with less practical matters. For example, you once made a list of numbers describing the lengths of sides of various right triangles. Others have made tables of very good fractional approximations to square roots. Still others have listed approximate solutions to many equations. Some of your colleagues who are really good at measuring the number of degrees in an angle make long lists of the angles that describe where those wanderers are in the sky.
If you live in Mesopotamia, then your number system is based on the number 60. If you are in China, you use a system like ours with base 10, but again not with consistent positional notation. Some early Mayan city states in North and Central America used a positional number system with base 20 and also had a symbol for zero. The dates of these developments are not known.
What mathematics don't you and your colleagues do? You don't abstract. That is, you might be able to solve, in effect, lots of specific quadratic equations, but you don't represent the numbers abstractly (by letters) to come up with general formulas. You also don't distinguish between exact and approximate answers; for example, calculating the circumference of a circle by multiplying the diameter by 3 is close enough for government work.
That is, unless you live in Egypt, where you have a pretty good system of fractions, now called Egyptian fractions. To find the area of the circle you'd multiply the square of the radius by
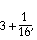
As a bureaucrat, scientist, mathematician, and priest rolled into one, you do computations primarily for the state. But after work, you go out and stare at the sky. Maybe there's a pattern in the movement of those wanderers.
Further Reading
Boyer, Carl B., A History of Mathematics (New York: John Wiley & Sons, 1968).
Campbell, Douglas, The Whole Craft of Number (Boston: Prindle, Weber & Schmidt, 1976).
Eves, Howard, An Introduction to the History of Mathematics
(Chicago: Saunders College Publishing, 1990).