Derivation of area of ellipse
To extend properties of circles to ellipses, we ask about the area of an ellipse.
The area of a circle of radius r is (pi)r 2. We might learn about ellipses if we recall how the formula for a circle can be derived.
In the Age of Application, the mathematicianArchimedes first proved the equivalent formula that the area of circle is half of the product of the radius by the circumference. In effect he did this with regular polygons inscribed in and circumscribed around the circle. He knew that the area of each polygon was a sum of areas of triangles that came to half the product of its apothem (like its radius) by its circumference. As the numbers of sides of the polygons increased, they became more and more like the circle, and on that basis he reached his conclusion.
Can we try something similar with an ellipse? It's not clear that an ellipse can be approximated closely with regular polygons, and it's not clear how to handle other polygons in a systematic enough way that we can keep track of their areas.
In effect, Archimedes was using what later came to be known as limits. And the mathematical area that extends work with limits is calculus. Can we use calculus to find the area of an ellipse?
Calculus relies on coordinate geometry. Calculus techniques can at least approximate the area of any region under the rectangular coordinate graph of a function. An ellipse isn't a graph of a function, but each quarter of it is. In fact, let's imagine an ellipse centered at the origin, with horizontal major axis of length 2a and vertical minor axis of length 2b . The area of such an ellipse is 4 times the area of the part of the ellipse in the first quadrant. And the area of that quarter is the area of the region under the graph of the ellipse over the interval from 0 to a on the x -axis.
But what's the function expression for that part of the ellipse? We can solve the rectangular coordinate equation of an ellipse for y, taking positive square roots since we're in the first quadrant. We get
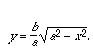
Therefore the area we seek can be expressed as the definite integral
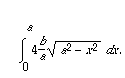
We might use a computer program to approximate this value. By hand we can get it exactly by a trigonometric substitution:
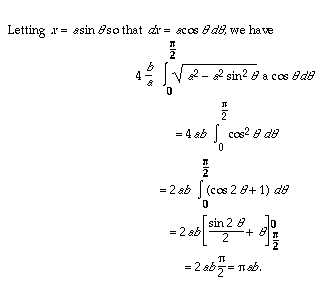
Thus we get a simple expression for the area of an ellipse!










