Derivation of reflection property
Let's try extending to ellipses the property of circles that the tangent line and radius to a point on a circle are perpendicular.
First we need to decide the elliptical analog of a circle's radius. An ellipse has a center, so the analog of a radius may be a line segment from the circle to the edge of the ellipse. Or, since the two foci are analogs to the center of the circle for some purposes, the analog to a radius may be a line segement from a focus to the ellipse.
If we draw pictures using the first approach, with line segments from the center to the ellipse, we see that they are not all perpendicular to the tangent lines.
Indeed, there's a lot of variety in the angles they make with the tangent lines. No pattern is apparent there.
The second approach is problematical because we have two lines from any point to the two foci. And neither of the lines is perpendicular to the tangent line.
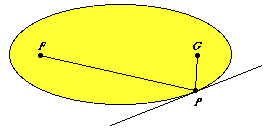
In deriving the constant sum property we find that the average of the lengths of the distances to the foci was always constant. In this case, could be be that the average angle between the tangent line and the two lines from the foci is a right angle?
How could we measure the angles to test this conjecture? We'd need to measure them against a fixed ray. How about the ray extending along the tangent line from the pont of tangency? Measured against that ray, the line to one focus makes an acute angle and the line to the other makes an obtuse angle. The mean, or average, angle, then, might very well be a right angle. In the picture, we're guessing that half of the sum of angles a + a +b is a right angle.

How might we prove this conjecture? Can we restate the conjecture in an equivalent form that's simpler? For the conjecture to be true, we must have a + a +b being a straight angle, or straight line. But a + c +b is a straight angle. So our conjecture is equivalent to the claim that angles a and c are equal.
Thus we're led to conjecture a new property of ellipses:











