Proof of constant ratio property of ellipse

This proof assumes that an ellipse is a figure satisfying the cylindrical section property.

Think of the cylinder as having a vertical axis, like a silo. Imagine all of the spheres that fit inside the cylinder and are tangent to the cylinder along a horizontal circle. One of these spheres is below the plane of the ellipse and tangent to it at a point. It intersects the cylinder in a circle of tangency

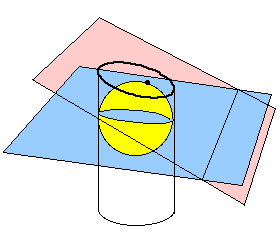
Let F be the point of tangency with the ellipse, and let P be an arbitrary point on the ellipse. Because the ellipse is not a circle, the plane of the ellipse and the plane containing the circle of tangency intersect in a line. Let Q be the point on that line nearest to P. We want to show that the ratio of distances PF/PQ is between 0 and 1 and is independent of P.

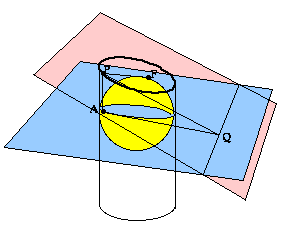
Consider the generating line of the cylinder that passes through P; let the point where it intersects the circle C be called A. Then the distance PF is the same as the distance PA because segments PF and PA are tangents from P to the same sphere. Therefore the ratio in which we're interested can be rewritten:

.

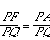But this ratio is the sine of the angle at Q in the triangle PQA. As the sine of an angle, the ratio is between 0 and 1. Moreover, the ratio is independent of P because the angle at Q is the angle between the two planes.