Ellipse: Proof assuming constant sum property

Given an ellipse, we need to construct a cylinder whose intersection with the plane of the ellipse is the ellipse itself.

To construct a cylinder, we must specify an axis and a radius.

For the axis, first imagine a plane perpendicular to the plane of the ellipse and through its major axis. Along that perpendicular plane, through either focus, construct a line perpendicular to the major axis. Now let's say that the length of the semi-minor axis of the given ellipse is b. At a distance b along that line that is perpendicular to the major axis, put a point P. The line through P and the center of the ellipse will be the axis of a cylinder.

For the radius of the cylinder, choose the length b.

We've shown elsewhere that the intersection of this cylinder with the plane of the ellipse is a figure satisfying the constant sum property. But is the intersection the same as the given ellipse? To show that it is, we show that the two foci are the same and the constant sums are the same.

We know that the foci of the intersection are the points of tangency to the plane of inscribed spheres. But the point P was constructed so that its distance from a focus of the given ellipse is b, and the cylinder was constructed of radius b. So a sphere of radius b centered at P will be inscribed in the cylinder and tangent to the ellipse at its focus. Therefore this focus of the given ellipse corresponds to a focus of the intersection. A similar argument with the sphere on the opposite side of the ellipse tells us that the two foci correspond.

Why are the two constant sums the same? They are both the lengths of the major axes of the respective figures. If we can see why the constructed cylinder passes through the endpoints of the major axis of the given ellipse, we'll know that the major axes of the two figures coincide and hence their lengths are the same.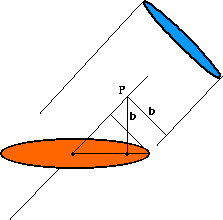

How far is the endpoint of the major axis from the cylinder's axis? It's a leg of a right triangle, one of whose non-right angles is the angle of the axis with the plane of the ellipse, and the hypotenuse of which is the length of the semi-major axis. But there's another such right triangle in the figure: the triangle whose vertices are P, the focus, and the center of the ellipse. Therefore the endpoint of the major axis is a distance b from the axis, so the cylinder passes through the endpoint.

By a similar argument, the other endpoint of the major axis lies on the cylinder as well. Hence the major axis of the given ellipse coincides with the major axis of the intersection of the cylinder with the plane. We can conclude that the two constant sums are the same and therefore that the figures coincide.